Breaking ADAM¶
In case you haven’t heard, one of the top papers at ICLR 2018 (pronounced: eye-clear, who knew?) was On the Convergence of Adam and Beyond. In the paper, the authors determine a flaw in the convergence proof of the ubiquitous ADAM optimizer. They also give an example of a simple function for which ADAM does not converge to the correct solution. We’ve seen how torchbearer can be used for simple function optimization before and we can do something similar to reproduce the results from the paper.
Online Optimization¶
Online learning basically just means learning from one example at a time, in sequence. The function given in the paper is defined as follows:
\(f_t(x) = \begin{cases}1010x, & \text{for } t \; \texttt{mod} \; 101 = 1 \\ -10x, & \text{otherwise}\end{cases}\)
We can then write this as a PyTorch model whose forward is a function of its parameters with the following:
class Online(Module):
def __init__(self):
super().__init__()
self.x = torch.nn.Parameter(torch.zeros(1))
def forward(self, _, state):
"""
function to be minimised:
f(x) = 1010x if t mod 101 = 1, else -10x
"""
if state[tb.BATCH] % 101 == 1:
res = 1010 * self.x
else:
res = -10 * self.x
return res
We now define a loss (simply return the model output) and a metric which returns the value of our parameter \(x\):
def loss(y_pred, _):
return y_pred
@tb.metrics.to_dict
class est(tb.metrics.Metric):
def __init__(self):
super().__init__('est')
def process(self, state):
return state[tb.MODEL].x.data
In the paper, \(x\) can only hold values in \([-1, 1]\). We don’t strictly need to do anything but we can write a callback that greedily updates \(x\) if it is outside of its range as follows:
@tb.callbacks.on_step_training
def greedy_update(state):
if state[tb.MODEL].x > 1:
state[tb.MODEL].x.data.fill_(1)
elif state[tb.MODEL].x < -1:
state[tb.MODEL].x.data.fill_(-1)
Finally, we can train this model twice; once with ADAM and once with AMSGrad (included in PyTorch) with just a few lines:
training_steps = 6000000
model = Online()
optim = torch.optim.Adam(model.parameters(), lr=0.001, betas=[0.9, 0.99])
tbtrial = tb.Trial(model, optim, loss, [est()], pass_state=True, callbacks=[greedy_update, TensorBoard(comment='adam', write_graph=False, write_batch_metrics=True, write_epoch_metrics=False)])
tbtrial.for_train_steps(training_steps).run()
model = Online()
optim = torch.optim.Adam(model.parameters(), lr=0.001, betas=[0.9, 0.99], amsgrad=True)
tbtrial = tb.Trial(model, optim, loss, [est()], pass_state=True, callbacks=[greedy_update, TensorBoard(comment='amsgrad', write_graph=False, write_batch_metrics=True, write_epoch_metrics=False)])
tbtrial.for_train_steps(training_steps).run()
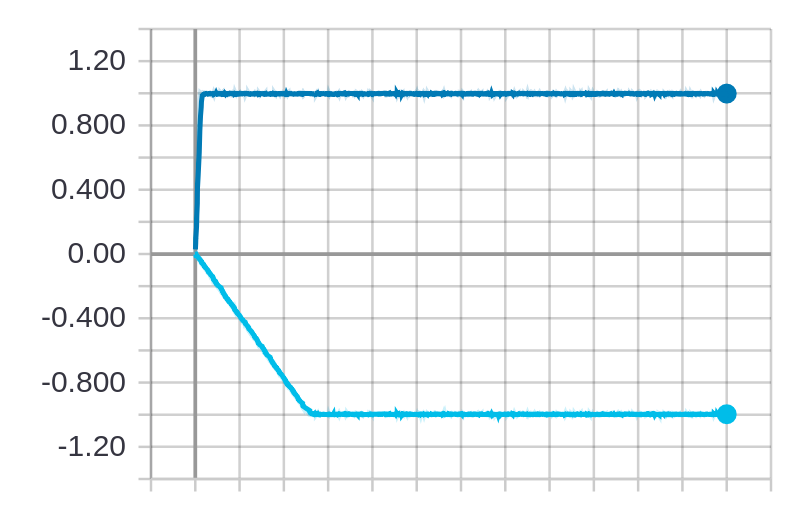
Note that we have logged to TensorBoard here and after completion, running tensorboard --logdir logs and
navigating to localhost:6006, we can see a graph like the one in Figure 1 from the paper,
where the top line is with ADAM and the bottom with AMSGrad:
Stochastic Optimization¶
To simulate a stochastic setting, the authors use a slight variant of the function, which changes with some probability:
\(f_t(x) = \begin{cases}1010x, & \text{with probability } 0.01 \\ -10x, & \text{otherwise}\end{cases}\)
We can again formulate this as a PyToch model:
class Stochastic(Module):
def __init__(self):
super().__init__()
self.x = torch.nn.Parameter(torch.zeros(1))
def forward(self, _):
"""
function to be minimised:
f(x) = 1010x with probability 0.01, else -10x
"""
if random.random() <= 0.01:
res = 1010 * self.x
else:
res = -10 * self.x
return res
Using the loss, callback and metric from our previous example, we can train with the following:
model = Stochastic()
optim = torch.optim.Adam(model.parameters(), lr=0.001, betas=[0.9, 0.99])
tbtrial = tb.Trial(model, optim, loss, [est()], callbacks=[greedy_update, TensorBoard(comment='adam', write_graph=False, write_batch_metrics=True, write_epoch_metrics=False)])
tbtrial.for_train_steps(training_steps).run()
model = Stochastic()
optim = torch.optim.Adam(model.parameters(), lr=0.001, betas=[0.9, 0.99], amsgrad=True)
tbtrial = tb.Trial(model, optim, loss, [est()], callbacks=[greedy_update, TensorBoard(comment='amsgrad', write_graph=False, write_batch_metrics=True, write_epoch_metrics=False)])
tbtrial.for_train_steps(training_steps).run()
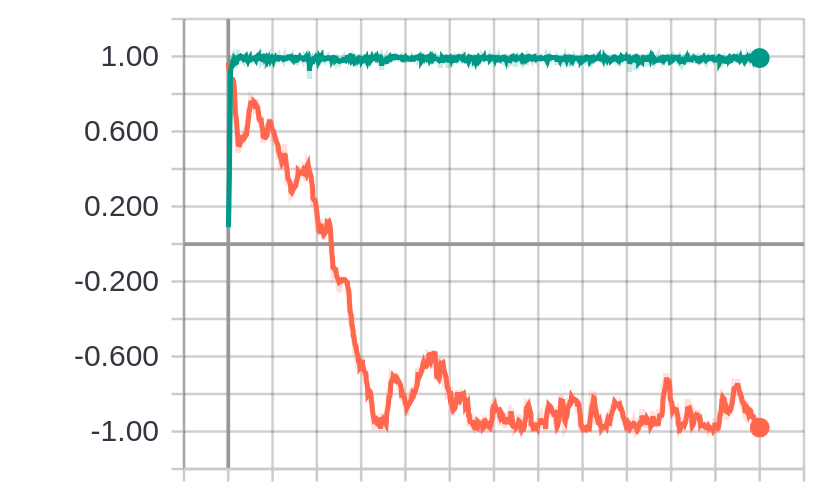
After execution has finished, again running tensorboard --logdir logs and navigating to
localhost:6006, we see another graph similar to that of the stochastic setting in Figure 1 of
the paper, where the top line is with ADAM and the bottom with AMSGrad:
Conclusions¶
So, whatever your thoughts on the AMSGrad optimizer in practice, it’s probably the sign of a good paper that you can re-implement the example and get very similar results without having to try too hard and (thanks to torchbearer) only writing a small amount of code. The paper includes some more complex, ‘real-world’ examples, can you re-implement those too?